Maya Calendar Calculations

Maya Calendar Calculations: A Web Tool for the Calculation and Reconstruction of Maya Dates and Astronomical Information in Maya Hieroglyphic Texts

Christian Prager (Rheinische Friedrich-Wilhelms-Universität, Bonn)
Tobias Mercer (Rheinische Friedrich-Wilhelms-Universität, Bonn)

As part of the Text Database and Dictionary of Classic Mayan research project, we have been working on a web tool for calculating and reconstructing calendar dates and astronomical information in Maya hieroglyphic texts since 2019. The tool is now available open access via the project website and allows users worldwide to perform calculations based on the Maya calendar. With this paper we would like to present our ideas regarding this software and provide users with a manual and some examples. The tool will be developed continuously during the project period and we are happy to receive suggestions and ideas for improvement. Currently, the tool can only be used for calculations that lie between the dates 0.0.0.0.0 4 Ahau 8 Cumku and 19.19.19.17.19 9 Cauac 12 Yaxkin, i.e. between September 8, 3114 BC and October 14, 4772 AD. In a future version, calculations into the distant past or the distant future will also be possible.

Calendar and astronomical data in the inscriptions

In the more than 150 years of research into Maya writing, first successes regarding the interpretation of their mathematical, calendrical and astronomical contents were achieved at the end of the 19th century . Ernst Förstemann discovered in the manuscripts and John Goodman in the stone inscriptions the structure and mechanism of three interlocked, cyclical as well as linear calendar systems, which were to later form the basis for the historical research of the Maya culture. The shortest cycle comprises 260 days and is still used today as a ritual and divination calendar. It is formed by the permutation of the numbers 1 to 13 with twenty day names, which result in 260 individual day designations. The solar calendar was already called Haab in the Classic period and has a length of 365 days. This cycle was composed of 18 months of 20 days each and a final month of 5 days. In the inscriptions, Tzolkin and Haab mostly appear together and with their elements constitute a calendar cycle that covers a total of 18980 days or 52 years. The Calendar Round allowed the scribes to exactly record a period of time within 52 years. Since, based on the arithmetic, a calendar round date would repeat itself after 52 years, the Maya introduced a continuous Day Count to unambiguously record a date or an event in time. The starting point of this linear system was a zero date, which was firmly interlocked with the Calendar Round Date 4 Ahau 8 Cumku and in original Maya notation read 13.0.0.0.0 4 Ahau 8 Cumku. This is a multiplicative-additive calendrical positional notation system in which each digit corresponds to a period of time, to which the numbers 0 - 19 are attached as multipliers. The calendrical number system is a so-called broken vigesimal system, which is principally based on 20, but with a calendrically necessary deviation from this base in the third position. Here the base 20 is not multiplied with the factor 20, but instead with 18. The following positions then again operate with the factor 20.

In addition to the function of the three calendars in the manuscripts, Förstemann also detected a 584-day Venus cycle in the Dresden Maya manuscript and proved that the Maya also calculated lunar and solar eclipses to the day. Based on Förstemann's arithmetic, Charles Bowditch, who first published algorithms for the simple calculation of Tzolkin, Haab and Long Count, discovered the function and arithmetic of so-called distance numbers in the inscriptions. These are the number of days passed between two calendrical entries in an inscription. Another important milestone for the study of Maya writing was reached by John Goodman, who first established the correlation between the Maya and Gregorian calendars, which is still valid today. It was later corrected by Juan Martínez and Eric Thompson by a few days to the constant 584285 (GMT correlation) and only recently recalibrated to 584286 days by Simon Martin and Joel Skidmore. In 1916, Sylvanus Morley identified the various elements of the so-called Supplementary Series, a sequence of formulaic hieroglyphs following the Long Count which are concluded by the Haab indication. The Supplementary Series contains a series of hieroglyphs with ritual and astronomical meanings, which Morley labeled with the letters from A-G and X. The meaning of these hieroglyphs remained unknown at first. In 1925 Eric Thompson discovered that the hieroglyphs F and G represented a cycle of 9 days. They form a cycle of successive days represented by nine different hieroglyphs, which runs independently of the other calendrical cycles, but is interlocked with them. The astronomical significance of the supplementary series was first recognized by John Teeple in 1931. According to him, the most important components were the hieroglyphs of the so-called lunar series, which are found directly following the hieroglyphs G and F between the Tzolkin and Haab indication of the initial series. Teeple calculated that the hieroglyphs E and D provided with coefficients indicate the moon age in whole days, i.e. how many whole days have elapsed since the last new moon. The length of the current lunar month of either 29 or 30 days was expressed by hieroglyph A, and closely related to hieroglyph A are hieroglyphs C and X. They indicated the number of elapsed lunar months within an 18-month lunar calendar calculated uniformly for the period 9.12.0.0.0 to 9.17.0.0.0. This time of the uniform lunar calendar is generally referred to as the "Period of Uniformity". The lunar calendars values can be predicted for this period by calculation with a deviation of about ± 3 days. A minor cycle of 7 days was discovered only in 1938 by Wyllys Andrews and its hieroglyphs named with the aliases Y and Z. A few years later, Eric Thompson discovered that the three known minor cycles of 7, 9, and 13 days constitute a major cycle of 819 days associated with four cardinal directions or colors. The combination of the four cycles creates a bigger cycle of 3276 days, which can be calculated arithmetically and is interlocked with the other calendrical cycles of the unification series.

Tzolkin, Haab, Calendar Round, the ritual cycles of 7 and 9 days as well as the 819 days cycle are, from an arithmetical point of view, independent ritual cycles, which are functionally interlocked with the linear day count calendar. The starting point for all calculations for the time between the zero date 0.0.0.0.0 (8.9.3114 BC) and the closing date 13.0.0.0.0 (21.12.2012 AD) of this calendar is the zero date, which correlates with the calendar round 4 Ahau 8 Cumku, the hieroglyph G9, the hieroglyph Y3, with the cardinal direction east and the day 3 in the 819-day cycle. The lunar calendar, which belongs to the supplementary series, is exclusively connected with the day count, but it can be subject to deviations of several days due to the purely visual observation of the celestial bodies. Therefore, the calculation of lunar phases and lunar months for a given date contains variations and requires the allowance of a tolerance of several days within the calculation.

A web tool for calculating calendar, distance and astronomical information in inscriptions

The arithmetic and correlation of the various calendrical and ritual cycles in the initial and supplementary series of Maya inscriptions and the consideration of a tolerance in the prediction of a lunar phase or determination of the lunar month for a given day opens up the possibility, when calculating calendar dates that are no longer legible, of reconstructing them to the day, narrowing them down to specific days or anchoring them to a specific period. As part of our project, a web-based tool has been under development since 2019 that performs all the complex calculations of the Maya calendar, giving the user the ability to calculate incomplete calendar dates in the inscriptions based on the readable text passages.
The tool in its current version (v1.0, 14.04.2021) consists of three basic functions for 1) calculating and converting calendar and astronomical information, 2) calculating multi-part distance information, and 3) calculating all solar eclipses in a specified time period. For each function, all calculated Maya dates are converted to the Gregorian or Julian calendar, the correlation constant can be changed as desired but uses the GMT correlation of 584285 days as default. In addition, the user can use the control panel to determine if a Maya date should be converted considering an astronomical Year Zero or traditionally based on the Gregorian/Julian calendar. Consequently, the zero date of the Maya calendar would fall on September 6, 3113 BC when converted astronomically and on September 6, 3114 BC traditionally.

Our calculations of the moon phase as well as solar and lunar eclipses are based on the one hand on Jean Meeus' astronomical algorithms, for which a given Maya date is first converted into the Julian day number using the correlation constant. On the other hand, the tool can calculate the age of the moon based on a given Maya date. The basis for this is an algorithm by Lawrence Roys that is still used today. It is based on the fact that the coefficients of the hieroglyph for the moon age (hieroglyph E and D) indicate the number of full days that have elapsed since the last new moon. Because the mean lunation duration is 29.53 days, the lunar age can be predicted based on a starting date for any date in Maya notation by calculation. The starting date for the lunar age calculation must correspond to a calendar date in Maya notation that can be shown to coincide with a new moon. The default starting date for this calculation is set to the date 9.17.0.0.0. According to two inscriptions from Quirigua and Piedras Negras a full solar eclipse took place on this day, so that the moon age on this day was exactly 0 days.

The moon age for any day in the Maya calendar is calculated by subtracting this start date from it and dividing the difference by 29.53 days. The result corresponds to the moon age, based on the starting point 9.17.0.0.0. In the Calendar Tool, users have the option to manually change the start date for the moon age calculation. Any Maya date can be used, but care should be taken that this day should coincide with a new moon. In the result output column, the astronomically calculated moon phase and the calculation of the moon age based on a Maya starting date are displayed in parallel and visualized graphically. In this way, users can check the validity of the lunar calculations and calibrate the results to each other by changing the correlation constant or the initial date. For example, if the user wants to calculate the astronomically exact moon phase for the date 9.17.0.0.0 and uses, say, the correlation constant of 584283 days, the tool calculates a moon age of 28.76 days for the day January 18, 771. According to hieroglyphic texts, however, the day 9.17.0.0.0 falls exactly on a new moon, meaning that a deviation of one day can be observed. However, if one changes the correlation constant to 584285 days, the tool calculates an exact astronomical new moon for this day (January 20, 771). The astronomically exact result for the day 9.17.0.0.0 based on the correlation 584285 thus coincides with the calculations of the Maya writers. The results for the calculation of solar eclipses in our Calendar Tool are similarly exact. Here the user has the possibility to set a correlation constant and to determine all dates within a period of 4 years, which fall on a visible solar eclipse, starting from a freely selectable Maya date. For the time being Chichen Itza has been defined as the observation site, in a later version the user will have the possibility to choose the observation site freely. With the help of the tool, inscribed solar eclipses can now be verified. According to the inscription on stela 1 from Santa Elena Poco Uinic a solar eclipse was visible on the day 9.17.19.13.16. Only using the correlation of 584286 days presented by Martin and Skidmore, the information from the inscription coincides with the astronomically exact calculation.

The study of hundreds of supplementary series reveals that the calculation of lunar data can be subject to multi-day fluctuations. Therefore, the calendar tool can take into account a tolerance of a specified number of days that the user can freely define. For example, if an incompletely obtained calendar date 9.?.0.?.15, 2 [day name] as well as the moon age 15 is available, the tool exactly calculates the Maya date 9.17.0.0.15 2 Men 8 Pop with a tolerance of 0 days. I.e. if the tolerance of the moon calculation is increased to ±1 day, all results where the moon age is calculated to be 14, 15 or 16 days are considered. This results in the possible Maya dates 9.7.0.12.15, 9.12.0.6.15 or 9.17.0.0.15 for the stated problem. If in this case the information about the moon age were also missing, 28 results would be possible for the incomplete Maya date 9.?.0.?.15 2 [Tzolk'in]; if we were also missing information about the day coefficient, the list of possible calculations would increase to 360 results. The more information can be filled in, be it ever so vague, the narrower the range of possible results. It is therefore necessary for a Calendar Tool to collect all available calendar information and in this way reduce the number of possible results.

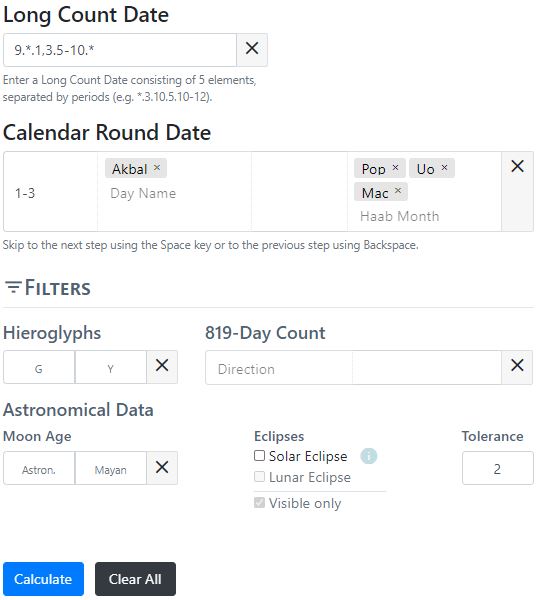
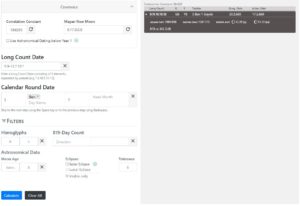
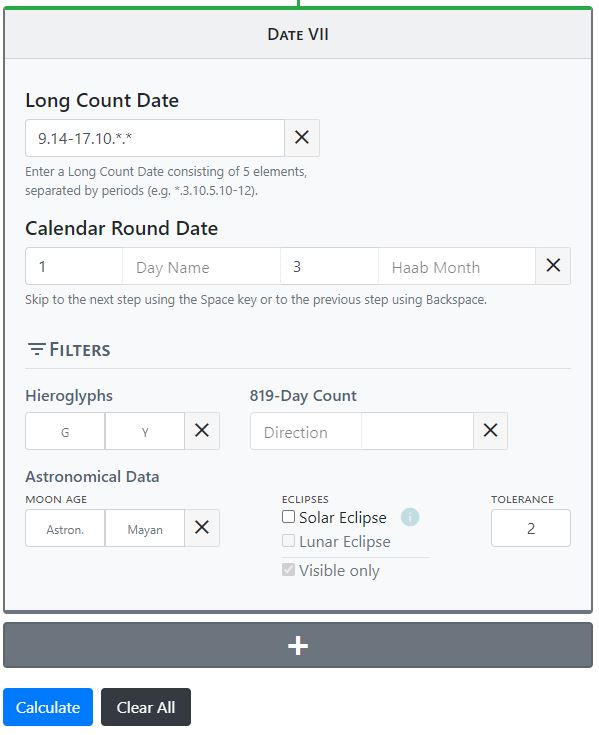
Often, when working with hieroglyphic texts, we encounter calendar information where the calculation does not provide distinct results. This might be because the date is cyclic or because the text is incompletely preserved and thus parts of the date information is only partially readable or completely lost. Many coefficients, day or month names or the distance number in these cases are not clearly identifiable and can in the best case be narrowed down to different numbers or names or to a certain number or name range. Missing or vague calendar information is therefore considered in the algorithm of the calendar calculations. For this purpose, the user has the possibility to enter missing, ambiguous, multiple values or number or name ranges in the input fields provided. In the current version of the tool (v.1.0, 14.04.2021) several input fields are available in the calculator for the calculation of a single date below the retractable control panel. In the control panel the user can define the correlation constant as well as the basis for the calculation of the moon age in Maya notation (i.e. the date of a new moon). For the input of Maya calendrical data the fields "Long Count Date" and "Calendar Round Date" are available in the current version. Unknown coefficients are entered either with * or a blank field, multiple coefficients are separated with commas " , " and number ranges are defined with " - ". In the following example, the coefficient of Katun would be unknown and is therefore marked with a blank field. Likewise, a " * " could be used here, as for example with the coefficient of the Kin position. In the Tun position, the coefficients 1 and 3 would be possible, separated here with a comma, and in the Winal position, all numbers from 5-10 would be possible. This open input possibility is also available for the coefficients of the hieroglyphs G and Y as well as for the Calendar Round. Accordingly, the user can also enter several calendar names to be considered in the calculation, in this case the months Pop, Uo and Mac. For the spelling of the day and month names, we use the colonial-era tradition, since the original reading of the day and month names has not yet been fully developed. However, users can also use alternative spellings of the month and day names, such as Ajaw for Ahau, Manik' for Manik, or Ok for Oc. The software now calculates six possibilities for this incomplete Maya date and additionally calculates the coefficients for the hieroglyphs G and Y. The respective date is converted into a decimal day number and subsequently correlated with the Julian and Gregorian calendar with the help of the correlation constant which can be set in the control panel.

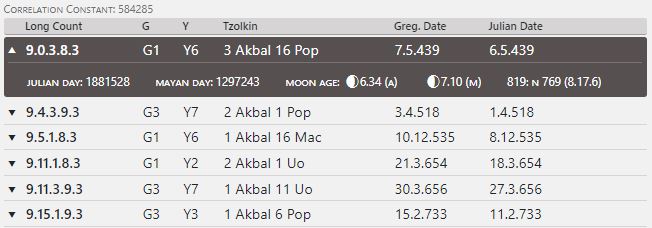
An illustrative example of the calculation of incomplete dates using our Calendar Tool can be found on Stela 6 from Yaxchilan. The calendar date in the initial series is no longer completely legible due to weathering, but the information in the supplementary series is complete. Identifiable elements from the initial and supplementary series include 10 Winal, 5 Ben, the hieroglyphs G6, D6, C3, X3, and the month coefficient 1. The month could be Uayeb, and the barely identifiable coefficient for Baktun would have to be 9, since the stela shows the ruler Bird Jaguar III ascending the throne at 9.9.16.10.13. The readable values from the initial and supplementary series are entered into the input fields as follows, the correlation constant in the control field is set to 584285 days and the date 9.17.0.0.0 serves as the basis for the moon age calculation.

The tool delivers three proposals for this incomplete calendar date in a result window, which now have to be checked individually.

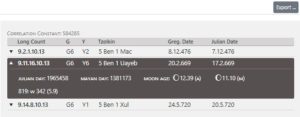
Users can view the suggestions in the tool itself or output them to PDF, TXT, XSLX and ODS formats for use with other software via an export function.

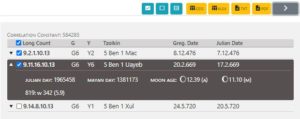
Among the delivered results there is also the date 9.11.16.10.13, 5 Ben 1 Uayeb. It confirms the observation that on Stela 6 the month name Uayeb is recorded. This date also falls into the lifetime of Bird Jaguar III. Accordingly we could have considered the rough lifetime of Bird Jaguar III between 9.9.0.0.0 and 9.12.0.0.0 to exclude results outside of this period. This way, the results are reduced from three to one choice.

Distance calculator

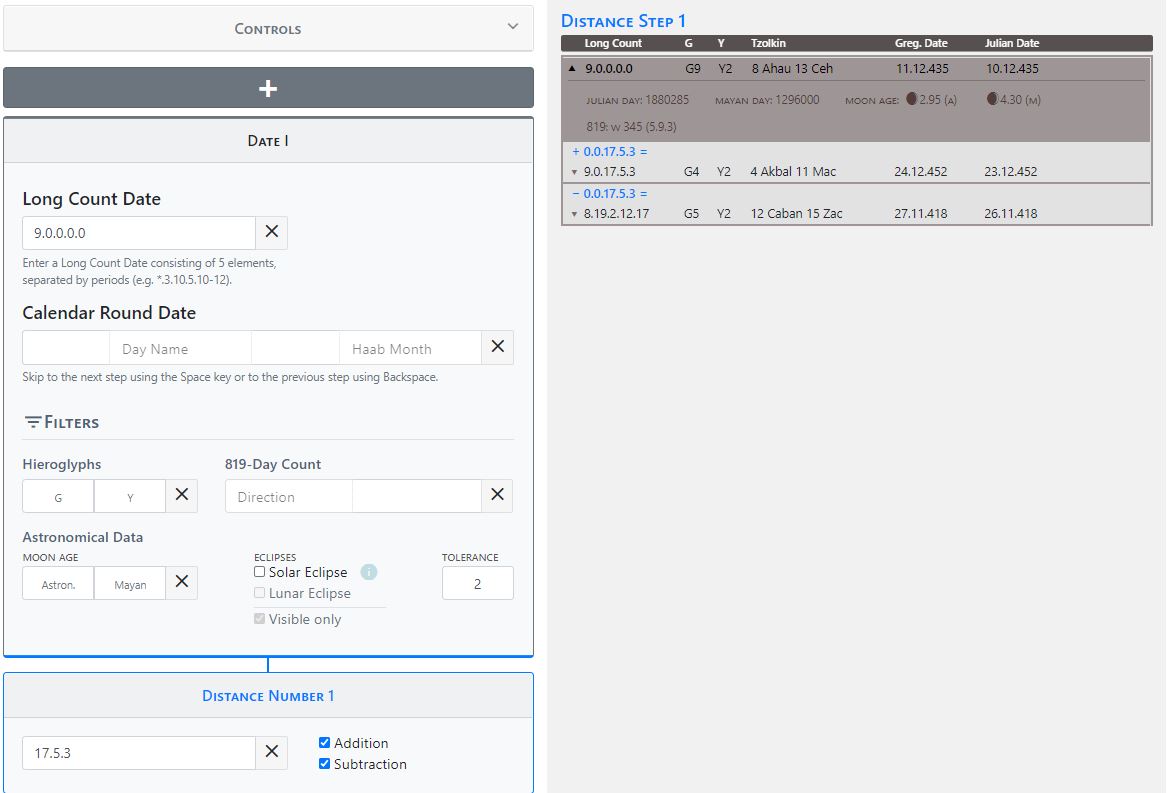
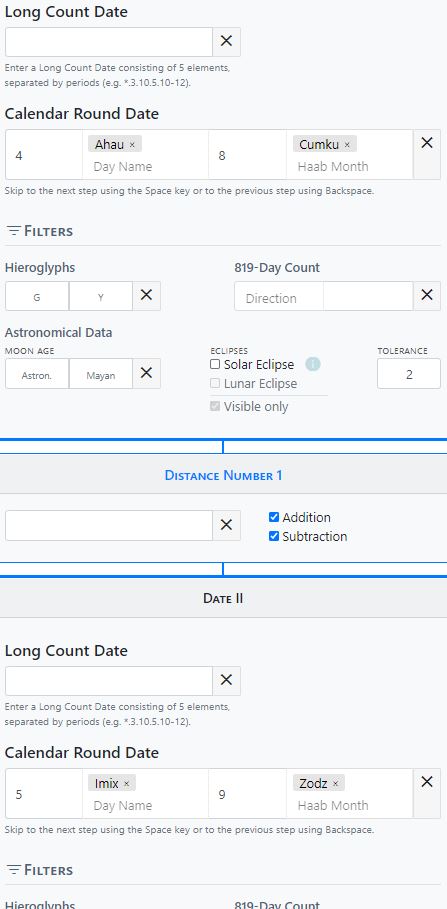
While the Calculator is used to calculate a single date, the second function "Distance" can be used to calculate the calendrical framework of an inscription. This generally consists of day number (Long Count), Calendar Rounds and distance numbers, which designate the number of days that lie between two calendar entries. If the first date is earlier than the subsequent date, the distance number is added to arrive at the later date. If, on the other hand, a later date refers to an earlier date, the distance number must be subtracted accordingly. Whether a distance number must be subtracted or added is sometimes indicated in the inscriptions by a hieroglyph, which Eric Thompson called "Anterior Date Indicator" (subtraction of the distance number) or "Posterior Date Indicator" (addition of the distance number). Since these indications are often missing in the inscriptions and distance numbers or calendar indications are often incomplete or unreadable, we have implemented both calculation methods in our Calendar Tool as the default setting. If you want to check the distance between two calendar entries, the tool works with both calculation methods simultaneously and displays them in the result output. Addition and subtraction can be deactivated and reactivated individually. Via the control panel already described above, the user can enter the desired correlation constant and the base date for the calculation of the moon age.

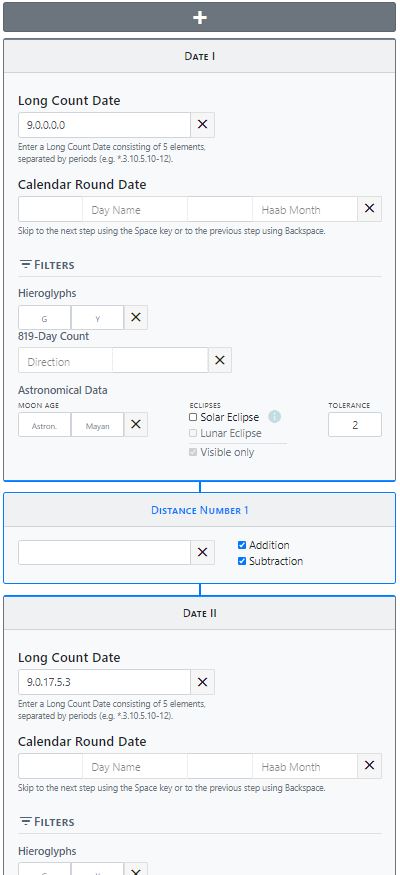
Distance numbers connect two calendar dates (date 1 and date 2), which are either present as day numbers (Long Count) or Calendar Rounds: Date 1 ± Distance Number = Date 2. Frequently, inscriptions contain several calendar dates and distance numbers connecting them, so that the distance number calculation is continued arbitrarily upward or downward: Date 1 ± Distance Number = Date 2 ± Distance Number = Date 3, etc. The user can not only transfer this calendar structure to the Calendar Tool and calculate it, but also has the possibility to perform a chain of calculations of any length. Users do not have to necessarily begin at the beginning of an inscription, but can for example start in the center or at the end of the text. If there is another date above the start date of the calculation, the user can click the gray "Plus button", which opens a new distance number calculation step above it. If, on the other hand, a distance number calculation is to follow below, the user activates the lower "Plus button", which opens a further distance number calculation step below. For the input of Maya calendrical data the fields "Long Count Date", "Calendar Round Date" and the hieroglyphs G and Y are available. In addition, information about the age of the moon and solar eclipses can be entered. If corresponding data is available for a date, they can be entered in the input field provided for this purpose. The distance number itself is entered in the field "Distance Number" between the two date specifications. Here, too, it is possible to work with vague information and variables: missing information is entered either with * or an empty field, multiple coefficients are separated with commas " , " and number ranges are defined with " - ". Multiple calendar names can also be entered and queried.

Basically, the distance calculator performs two types of calculations: 1) calculation of the distance number: calculates the number of days between two given calendar positions, (arithmetic: distance number = date 1 - date 2) and 2) calculation of the date: calculates a calendar date starting from a given calendar date and a known distance number (arithmetic: date 2 = date 1 ± distance).

Calculation of Distance: between 9.0.0.0.0 and 9.0.17.15.3

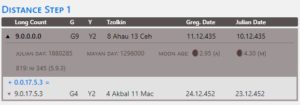
In the result column the results of the calculations are displayed. Besides the conversion to our western calendar we find for each Maya date the indication of the moon age according to astronomically exact calculations (left) and based on a Maya date (right, in this case based on 9.17.0.0.0), each with graphical representation of the moon phase. The closer the results of both moon calculations are to each other, the more exact the chosen correlation between Maya date and our calendar or the calculation of the moon age by the Maya astronomers is.

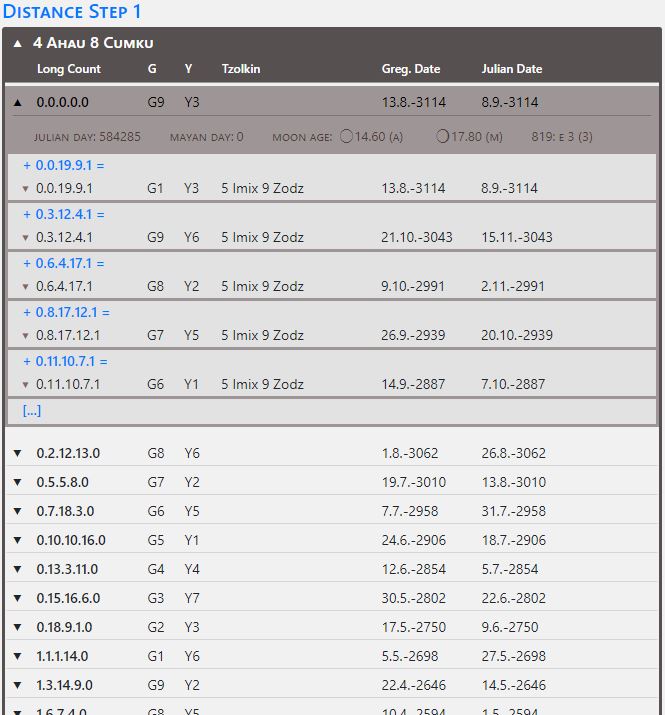
The tool also allows calculating the distance number between two given Calendar Rounds, e.g. 4 Ahau 8 Cumku and 5 Imix 9 Zodz. For this purpose, this information is entered into the input fields for the Calendar Round. The tool calculates not only the shortest distance between the given Calendar Rounds, but all possible day numbers in the period between 0.0.0.0.0 and 9.19.19.17.19. The result can be narrowed down by entering additional information in the field "Long Count" or for the Hieroglyphs G, Y as well as the moon age.

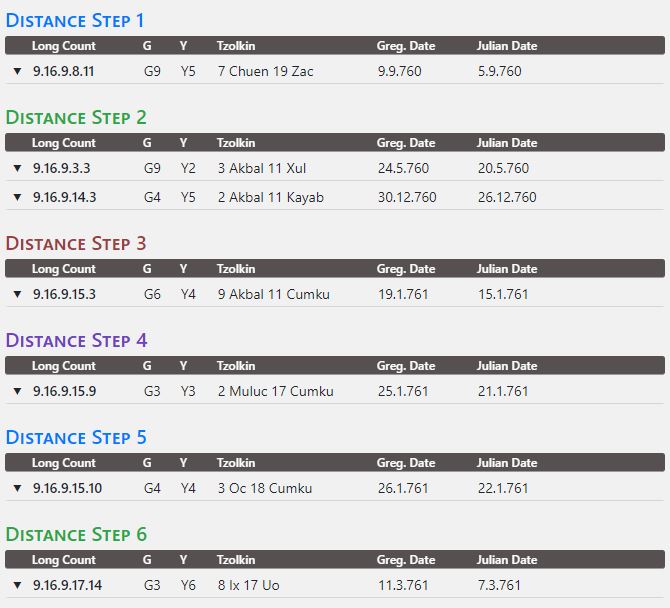
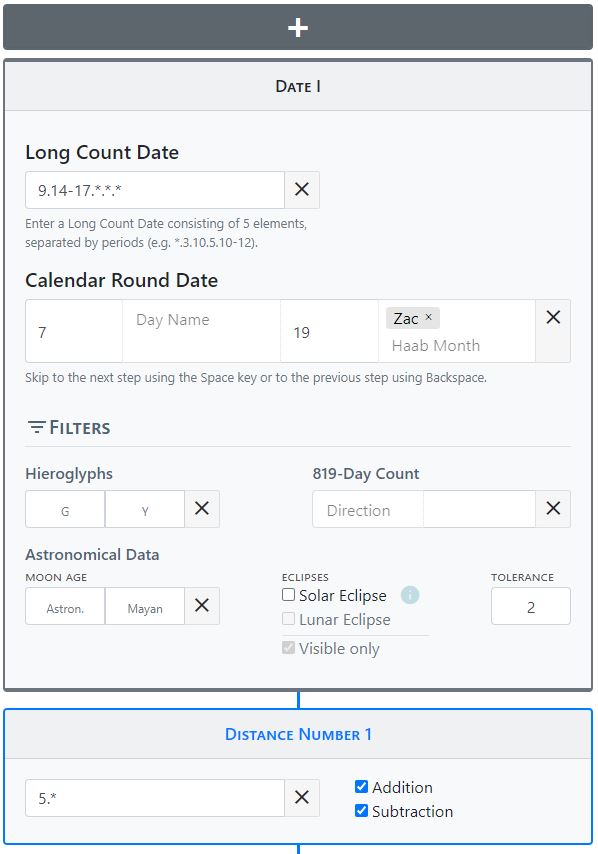
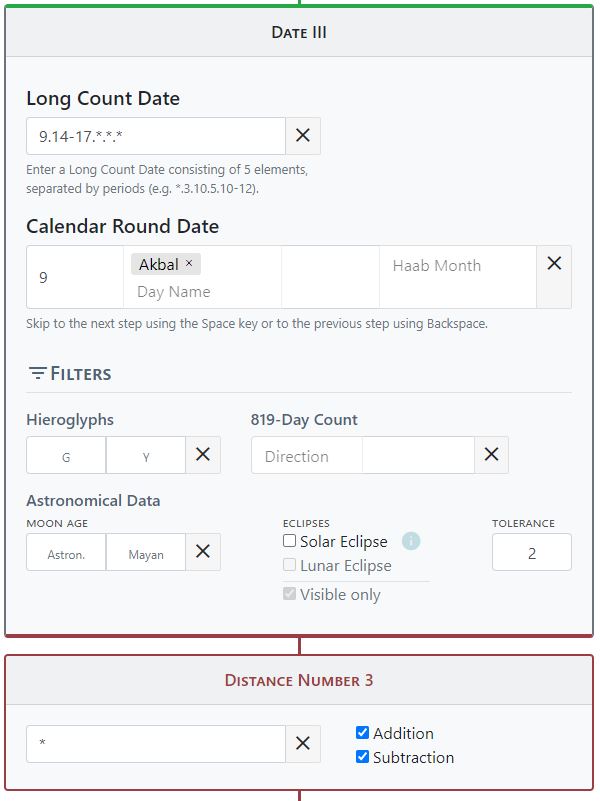
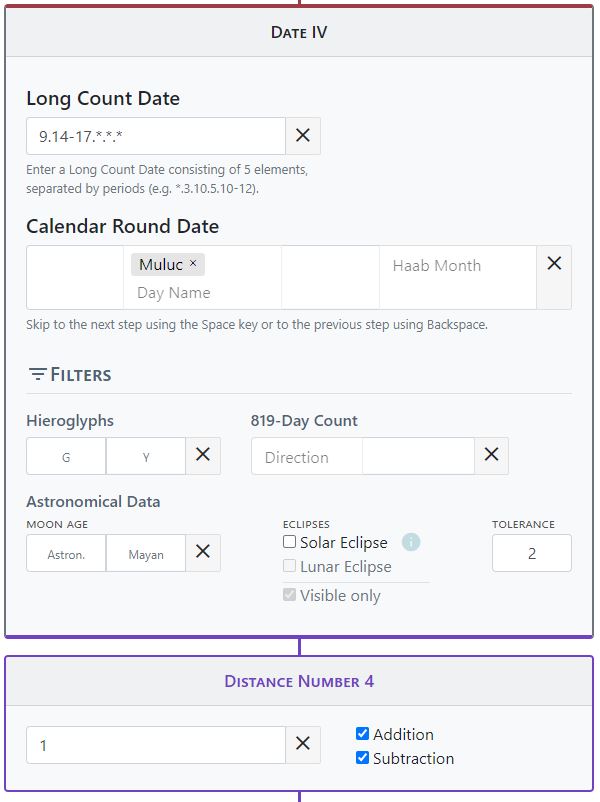
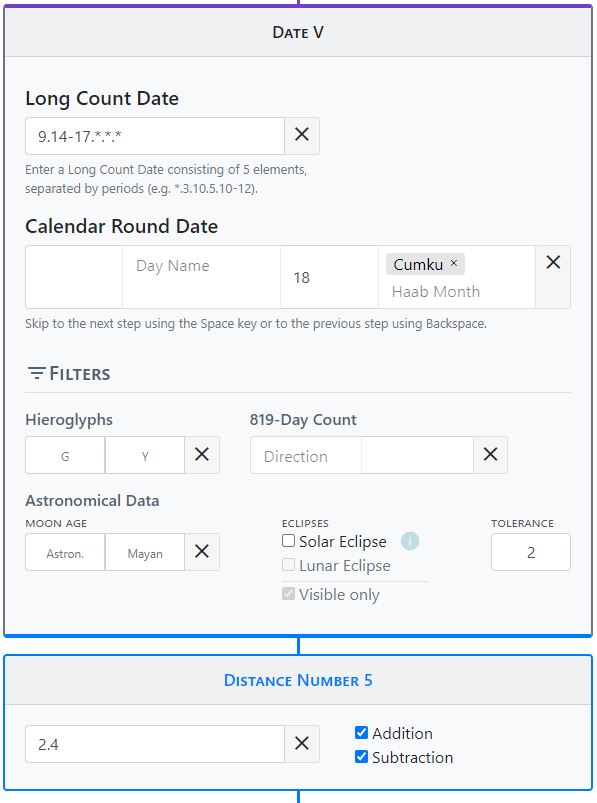
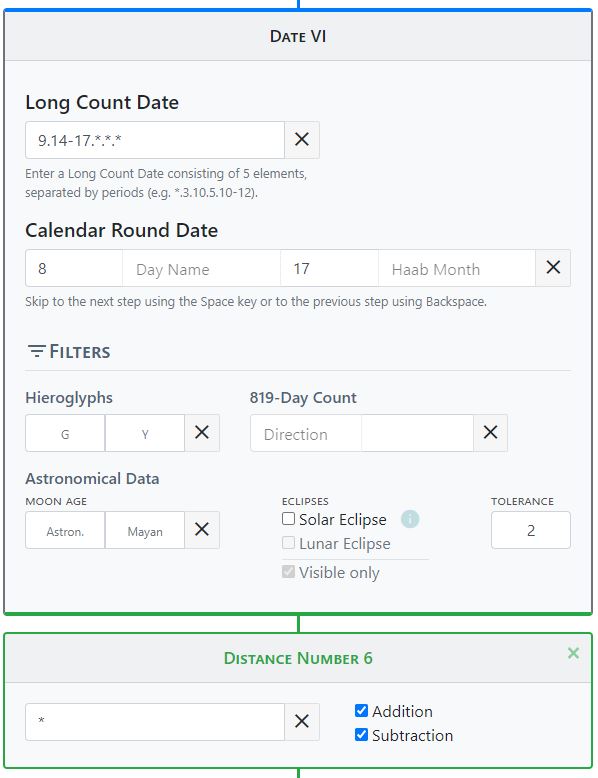
Many texts are only partially legible due to weathering, and calendar information and distance numbers are often fragmentary or missing entirely. With the help of our distance number calculator, however, many of the missing parts can be filled in automatically by transferring the calendar information present in an inscription to the distance number calculator. The algorithm calculates all possible combinations of the different calendars and matches them with the existing calendar information. A good calculation example is the text on the Hieroglyphic Stairway 2 from Tamarindito. The calendar framework of this inscription shows considerable gaps in the day numbers as well as Calendar Rounds, which the distance number calculator is able to reconstruct. The dates on the stairway can be narrowed down between 9.14.0.0.0 and 9.17.0.0.0 based on Tamarindito's history. This information is entered into the tool. The readable calendar framework of Hieroglyphic Stairway 2 is as follows.

__.__.__.__.__     7  ____ 19 Zac

          5.__

__.__.__.__.__     __ Akbal __ ___

         __.__

__.__.__.__.__     9  Akbal __ ___

           .__

__.__.__.__.__     __ Muluc __ ___

           . 1

__.__.__.__.__     __ ___ 18 Cumku

           2.4

__.__.__.__.__     8 ___ 17 ___

           .__

__.__.10.__.__     1 ___ 3 ___

This information is transferred to the calendar tool as follows.

The result is as follows and in accordance with calculations published in the literature.